UN 2015 matematika !PA

pada tanggal

  1. Diketahui premis-premis:(1) Tuti tidak mempunyai keberanian atau ia akan menang.
    (2) Tuti tidak akan menang

    kesimpulan yang sah dari premis-premis tersebut adalah ... 
         a. Tuti mempunyai keberanian 
         b. Tuti tidak mempunyai keberanian
         c. Tuti takut
         d. Tuti tidak takut
         e. Tuti tidak percaya diri
  2. Pernyataan "Jika semua guru tidak mengajar,maka beberapa siswa gembira" setara dengan ...
        a. Beberapa guru mengajar atau beberapa siswa gembira dan
            semua guru mengajar.
        b. Beberapa siswa gembira dan semua guru mengajar
        c. Beberapa guru mengajar atau semua siswa gembira
        d. Semua siswa tidak gembra atau semua guru tidak
            mengajar
        e. Semua guru tidak gembira dan ada guru yang mengajar
  3. Bentuk sederhana dari    {\left( {\frac{{3{x^{\frac{3}{2}}} \cdot {y^{ - \frac{4}{3}}} \cdot {z^{ - \frac{4}{5}}}}}{{2{x^{ - \frac{7}{2}}} \cdot {y^{ - \frac{1}{3}}} \cdot {z^{\frac{6}{5}}}}}} \right)^2}   adalah ...

         a.      {\frac{{3{x^2}}}{{2{y^{}} \cdot {z^2}}}}         b.  {\frac{{9{x^5}}}{{4{y^{}} \cdot {z^2}}}}        c.  {\frac{{3{x^5}}}{{2{y^{}} \cdot {z^2}}}}        d.  {\frac{{9{x^{10}} \cdot y}}{{4{z^2}}}}         e.  {\frac{{9{x^{10}}}}{{4{y^2} \cdot {z^2}}}}
  4. Bentuk sederhana (3+2)(3−2)5+2 adalah ….         
         a.  2\left( {\sqrt 5 - 2} \right)                    c.  \left( {\sqrt 5 - 2} \right)                              e.  \frac{1}{2}\left( {\sqrt 5 - 2} \right)       
         b.  \frac{1}{4}\left( {\sqrt 5 - 2} \right)                    d.   - \left( {\sqrt 5 - 2} \right)
  5. Hasil    \frac{{{}^6\log \sqrt 5 \cdot {}^{25}\log 36 + {}^7\log \frac{1}{{49}}}}{{2\log 4\sqrt 2 + {}^2\log 16}}      adalah ...

      a.   - \frac{3}{{13}}          b.   - \frac{{39}}{4}           c.   - \frac{{13}}{4}          d.   - \frac{1}{{13}}              e.  - \frac{1}{{26}}
  6. Persamaan kuadrat  {x^2} - 5x + 7 = 0 akar- akarnya adalah  \alpha  dan  \beta  . Persamaan kuadrat yang akar-akarnya  \alpha + 3  dan  \beta + 3  adalah ...
         a.  {x^2} - 11x + 31 = 0
         b.  {x^2} + x + 13 = 0
         c.  {x^2} - 2x + 10 = 0
         d.  {x^2} - 11x - 31 = 0
         e.  {x^2} + 11x + 31 = 0
  7. Persamaan kuadrat   {x^2} - 6px - 2x + 14p + 21 = 0    mempunyai dua akar real. Batasan nilai  p yang memenuhi adalah...

    a.  p \le \frac{{10}}{9}\,\,\,atau\,\,\,p \ge 2          c.   - 2 \le p \le \frac{{10}}{9}               e.  p \ge \frac{{10}}{9}\,\,\,atau\,\,\,p \le - 2

    b.  p \le - \frac{{10}}{9}\,\,\,atau\,\,\,p \ge 2       d.  - \frac{{10}}{9} \le p \le - 2
  8. Adi, Budi, Cici, dan Dedi pergi ke toko koperasi sekolahnya membeli buku tulis, pena, dan pensil dengan merek yang sama.
    • Adi membeli 3 buku tulis, 1 pena, dan 2 pensil dengan harga  Rp. 22. 000,00
    • Budi membeli 2 buku tulis, 3 pena,dan 1 pensil dengan harga  Rp. 28.000,00.
    • Cici membeli 1 buku tulis, 2 pena, dan 3 pensil dengan harga  Rp. 22.000,00.
    Dedi membeli 2 buku tulis, 1 pena, dan 1 pensil, maka ia harus membayar ….
     a. Rp. 14.000,00           c. Rp. 20.000,00          e. Rp. 16.000,00
     b. Rp. 18.000,00           d. Rp. 17.000,00
  9. Persamaan lingkaran yang berpusat di (-2,3) dan menyinggung garis x - 2y - 7 = 0 adalah ...
       a.  {x^2} + {y^2} + 2x - 3y - 4 = 0                     d.  {x^2} + {y^2} - 4x + 6y + 32 = 0
       b.  {x^2} + {y^2} - 2x + 3y + 4 = 0\,                    e.  {x^2} + {y^2} + 4x - 6y - 32 = 0
       c.  {x^2} + {y^2} + 4x - 6y + 9 = 0
  10. Salah satu persamaan garis singung lingkaran  {x^2} + {y^2} - 4x + 6y + 3 = 0  yang tegak lurus dengan x + 3y + 2 = 0 adalah ...
         a. 3x - y + 1 = 0                                  d. 3x - y - 1 = 0
         b. 3x - y + 7 = 0                                  e. 3x - y - 13 = 0
         c. 3x - y + 19 = 0
  11. Suku banyak  P(x) = {x^3} + 2{x^2} + px + q jika dibagi dengan  \left( {{x^2} - x - 2} \right)mempunyai sisa (3x - 1). Nilai (p - q) adalah ...
            a. -8         b. -9          c. -5            d. 5        e. 9
  12. Salah satu faktor dari persamaan suku banyak  2{x^3} - 5{x^2} - px + 3 = 0 adalah (x + 1). Faktor yang lain dari persamaan suku banyak itu adalah ...
           a. x + 2 dan 2x - 1
           b. 2x - 1 dan x - 3
           c. x + 3 dan x + 2
           d. 2x + 1 dan x - 2
           e. x - 2 dan x - 3
  13. Diketahui  f(x) = {x^2} - 4x + 6 dan g(x) = 2x +3. Fungsi komposisi
    (f o g) = ...?
         a.   4{x^2} + 4x + 15
         b.  2{x^2} - 8x + 15
         c.  2{x^2} - 8x + 12
         d.  4{x^2} + 4x + 3
         e.  4{x^2} + 4x + 27
  14. Seorang pedagang kue akan menjual dua jenis kue. Harga setiap kue A Rp. 3.000,00 dan dijual memperoleh keuntungan Rp. 1.000,00/ buah, sedangkan harga kue B adalah Rp. 4.000,00 dan dijual memperoleh keuntungan Rp. 1.500/buah. Modal yang tersedia adalah Rp. 1.700,00 dan paling banyak hanya menjual 500 kue setiap hari. Jika kue tersebut terjual habis, maka keuntungan maksimum yang diperoleh pedagang kue tersebut adalah ...
         a. Rp. 700.000,00
         b. Rp. 650.000,00
         c. Rp. 600.000,00
         d. Rp. 500.000,00
         e. Rp. 750.000,00
  15. Diketahui matriks A = \left( {\begin{array}{ccccccccccccccc} { - 2}&x\\ 6&3 \end{array}} \right) ,  B = \left( {\begin{array}{ccccccccccccccc} { - 5}&{14}\\ y&{ - 2} \end{array}} \right)  dan  C = \left( {\begin{array}{ccccccccccccccc} z&{ - 1}\\ 1&5 \end{array}} \right) . Jika A - B = C, maka x + y + z = ...
    a. 10            b. 15            c. 18               d. 20               e. 25
  16. Diketahui vektor  a = \left( {\begin{array}{ccccccccccccccc} p\\ 2\\ 1 \end{array}} \right) ,  b = \left( {\begin{array}{ccccccccccccccc} 4\\ { - 3}\\ 6 \end{array}} \right) ,  c = \left( {\begin{array}{ccccccccccccccc} 2\\ { - 1}\\ 3 \end{array}} \right) . Jika a tegak lurus b maka hasil dari 2a - b + c  adalah ...
            a. 3i  + 4j  - 4k                d. 3i  + 4j  - 5k
            b. 4i  + 4j  - 5k                e. 4i  + 6j  - 5k
            c. 3i  + 6j  - 4k
  17. Dikeahui | a | = 3; | b | = 4; | a + b | = 7. Jika  \theta  adalah sudut antara vektor a dan b maka nilai sin  \theta  adalah ...
    a. 1          b. 2/3       c. 1/2        d. 0       e. 1/3
  18. Diketahui vektor u = 3i - pj - 4k dan  v = 2i + 6j - 3k.Apabila panjang proyeksi vektor u pada v adalah 6, maka nilai p adalah ...
    a. -4      b. -6        c. -5         d. -10        e. -8
  19. Pada transformasi pencerminan terhadap garis y = x dilanjutkan dengan rotasi pusat O (0,0) sebesar  {{{90}^0}}  berlawanan arah dengan jarum jam. Bayangan dari garis 2x - 3y -1 = 0 mempunyai persamaan ...
    a. 2x - 3y + 1 = 0                   d. 3x + 2y + 1 = 0
    b. 3x + 2y - 1 = 0                  e. 2x + 3y + 1 = 0
    c. 2x + 3y - 1 = 0
  20. Penyelesaian dari  {}^{\frac{1}{2}}\log ({x^2} - 3x + 2) < {}^{\frac{1}{2}}\log (10 - x)   adalah ....

    a. 2 < x < 10   atau x < -2
    b. -2 < x < 10   atau x >10c. 4 < x < 10   atau x < -2d. 2 < x < 10   atau -2 < x < 1e. x >10  atau x < 2
  21. Jika diketahui fungsi  xyz = {2^6}  dan  \left( {{}^2\log x} \right) \cdot \left( {{}^2\log yz} \right) + \left( {{}^2\log y} \right) \cdot \left( {{}^2\log \,z} \right) = 10  untuk  x,y,z \ge 0 , maka
    \sqrt {{}^2{{\log }^2}x + {}^2{{\log }^2}y + {}^2{{\log }^2}z} =   ,,,
    a. 8         b. 6             c. 5                 d. 4                 e. 1
  22. Diketahui suku ke 3 dan suku ke 8 barisan aritmatika berturut-turut adalah 2 dan -13. Jumlah 20 suku pertama deret tersebut adalah ...
     a. - 380         b. - 490       c. = - 440        d. - 410         e. - 580 
  23. Diketahui kubus ABCD.EFGH dengan rusuk 6 cm. Jika K berada di tengah-tengah CG, maka jarak titik H ke BK adalah …
    a.  3\sqrt 5           b.  \frac{5}{6}\sqrt {30}         c.  \sqrt {30}          d.  3\sqrt 3           e.  3\sqrt 2
  24. Kubus ABCD.EFGH dengan rusuk 6 cm. Sinus sudut antara bidang AFH dengan bidang CFH adalah ….
    a.  \frac{1}{2}\sqrt 2          b.  \frac{1}{3}        c.  \frac{2}{3}\sqrt 2           d.  2\sqrt 2            e.  \sqrt 2
  25. Sebuah bola jatuh dari ketinggian 6 m dan memantul kembali dengan 3/4 kali tinggi semula. Panjang lintasan gerak bola sampai berhenti adalah ….|
    a. 18 m         b. 42 m        c. 36 m        d. 24 m       e. 48 m
  26. Himpunan penyelesaian dari persamaan
    cos 2x + 3 sin x - 2 = 0 dalam  {0^o} \le x \le {360^o} adalah ...
    a.  \{ {30^o}{,90^o}\}                              d.  \{ {150^o}{,300^o}\}               
    b.  \{ {30^o}{,90^o}{,150^o}\}                        e.   \{ {30^o}{,150^o}\}
    c.  \{ {30^o}{,90^o}{,120^o}\}
  27. Diketahui sudut A dan B lancip dengan  \cos (A + B) = \frac{3}{4}   dan  \cos A \cdot \cos B = \frac{2}{3}  . Nilai   \tan A \cdot \tan B  adalah ...
    a. 1/8      b. -1/12      c. -1/8      d. 1/12      e. -1/4
  28. Perhatikan gambar!
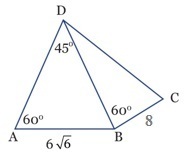
    Panjang DC adalah ….

    a.  12\sqrt 3        b.  2\sqrt {57}           c.  10\sqrt 3        d.  2\sqrt {63}        e.  2\sqrt {61}
  29. Nilai dari   {\lim }\limits_{x \to \infty } \left( {\sqrt {{x^2} - 6x + 9} - \left( {x - 2} \right)} \right)  adalah ....
    a. 0       b. -2       c. 2      d. 1       e. -1
  30. Nilai dari  {\lim }\limits_{x \to \infty } \frac{{x \cdot \tan 4x}}{{2 - 2{{\cos }^2}x}}

    a. 2        b. -1/2     c. 0      d. 1      e. 1/2
  31. Icha akan meniup balon karet berbentuk bola. Ia menggunakan pompa untuk memasukkan udara dengan laju pertambahan volume udara  40\,\,c{m^3}/dtk Jika laju pertambahan jari-jari bola  20\,\,c{m^3}/dtk  jari-jari bola setelah ditiup adalah ….         
    a.  \frac{1}{{2\sqrt \pi }}           b.  \frac{1}{{\sqrt \pi }}              c.  \frac{2}{{3\sqrt \pi }}            d.  \pi               e.  \frac{1}{{\sqrt {2\pi } }}
  32. Hasil  \int {18{x^2}{{\left( {2{x^3} - 3} \right)}^5}dx}   adalah ...
    a.  \frac{3}{2}{\left( {2{x^3} - 3} \right)^6} + C           d.  \frac{1}{2}{\left( {2{x^3} - 3} \right)^6} + C
    b.  \frac{3}{2}{\left( {3{x^3} - 2} \right)^6} + C           e. \frac{1}{2}{\left( {3{x^3} - 2} \right)^6} + C
    c.   \frac{1}{3}{\left( {2{x^3} - 3} \right)^6} + C       
  33.    Nilai dari  \int\limits_1^4 {\left( {5\sqrt x - \frac{1}{{2\sqrt x }}} \right)dx}   adalah ...

    a.  18\frac{2}{3}      b.  17\frac{1}{3}      c.  15\frac{1}{4}       d.  22\frac{1}{3}       e.  25\frac{1}{4}
  34. Hasil dari  \int {4\sin 5x \cdot \cos 3x\,} dx adalah ...
    a.   - \frac{1}{2}\cos 8x - 2\cos 2x + C                 d.  \frac{1}{4}\cos 8x - \cos 2x + C
    b.    - 2\cos 8x - 2\cos 2x + C                e.  \frac{1}{2}\cos 8x - \cos 2x + C
    c.   - \frac{1}{4}\cos 8x - \cos 2x + C
  35. Nilai dari  \int\limits_{ - \pi /2}^{\pi /2} {\left( {6\cos 3x - 3\sin 3x} \right)dx}   adalah ...
    a. -2       b. -6        c. 2         d. 0          e. -4
  36. Luas daerah yang dibatasi  y = {x^3} - 6{x^2} + 8x  dan sumbu X
    a. 4 satuan luas                      d. 2 satuan luas
    b. 16 satuan luas                    e. 12 satuan luas
    c. 8 satuan luas
  37. Volume benda putar terjadi jika daerah antara kurva  y = - {x^2} + 9sumbu X dan garis x = 0 di kuadran I diputar mengelilingi sumbu X sejauh  {360^0}  adalah ... satuan luas
    a.  48\frac{3}{5}\pi         b.   129\frac{3}{5}\pi        c.  72\frac{2}{5}\pi       d.  81\frac{3}{5}\pi       e.  18\pi
  38. Perhatikan histogram berikut!

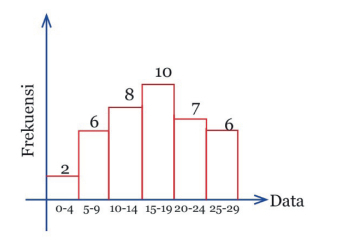
    Modus dari data pada histogram di atas adalah ….
    a, 16,25      b, 15,50         c, 14,50         d, 15,25         d,16,50
  39. Dari 10 orang pengurus suatu organisasi akan dipilih sebagai ketua, sekertaris, dan bendahara. Banyak cara pemilihan yang mungkin adalah ....
    a. 40     b. 720       c. 256       d. 5040       e. 210
  40. Seorang penjaga gawang profesional mampu menahan tendangan penalti dengan peluang 3/5. Dalam sebuah kesempatan dilakukan  5 kali tendangan peluang penjaga gawang mampu menahan 3 kali tendangan penalti tersebut adalah ...
    a.  \frac{{216}}{{625}}       b.  \frac{{228}}{{625}}          c.  \frac{{612}}{{625}}        d.  \frac{{180}}{{625}}        e.  \frac{{230}}{{625}}

Komentar

Posting Komentar